6.1. Теория

Во время своей работы программы используют различные структуры данных и алгоритмы, в связи с чем обладают разной эффективностью и скоростью решения задачи. Дать оценку оптимальности решения, реализованного в программе, поможет понятие вычислительной сложности алгоритмов.

6.1.1. Основные понятия

Вычислительная сложность (алгоритмическая сложность) - понятие, обозначающее функцию зависимости объема работы алгоритма от размера обрабатываемых данных.

Вычислительная сложность пытается ответить на центральный вопрос разработки алгоритмов: как изменится время исполнения и объем занятой памяти в зависимости от размера входных данных?. С помощью вычислительной сложности также появляется возможность классификации алгоритмов согласно их производительности.

В качестве показателей вычислительной сложности алгоритма выступают:

1. Временная сложность (время выполнения).

   Временная сложность алгоритма - это функция от размера входных данных, равная количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера.

   Временная сложность алгоритма зачастую может быть определена точно, однако в большинстве случаев искать точное ее значение бессмысленно, т.к. работа алгоритма зависит от ряда факторов, например, скорости процессора, набора его инструкций и т.д.

2. Асимптотическая сложность.

   Асимптотическая сложность оценивает сложность работы алгоритма с использованием асимптотического анализа.

   Алгоритм с меньшей асимптотической сложностью является более эффективным для всех входных данных.

6.1.2. Асимптотические нотации

Асимптотическая сложность алгоритма описывается соответствующей нотацией:

• О-нотация, \(O\) («О»-большое): описывает верхнюю границу времени (время выполнения «не более, чем…»);

• Омега-нотация, \(\Omega\) («Омега»-большое): описывает нижнюю границу времени (время выполнения «не менее, чем…»).

Например,

\[T(n) = O(N^{2})\]

говорит о том, что алгоритм имеет квадратичное время выполнения относительно размера входных данных в качестве верхней оценки («О большое от эн квадрат»).

Каждая оценка при этом может быть:

• наилучшая: минимальная временная оценка;

• наихудшая: максимальная временная оценка;

• средняя: средняя временная оценка.

При оценке, как правило, указывается наихудшая оценка.

Примечание

Допустим, имеется задача поиска элемента в массиве. При полном переборе слева направо:

• наилучшая оценка: \(O(1)\), если искомый элемент окажется в начале списка;

• наихудшая оценка: \(O(N)\), если искомый элемент окажется в конце списка;

• средняя оценка: \(O \left ( \cfrac{N}{2} \right ) = O(N)\).

6.1.2.1. Верхняя оценка и \(O\)-нотация

Наиболее часто используемой оценкой сложности алгоритма является верхняя (наихудшая) оценка, которая обычно выражается с использованием нотации O-большое.

Выделяют следующие основные категории алгоритмической сложности в \(O\)-нотации:

1. Постоянное время: \(O(1)\).

• Время выполнения не зависит от количества элементов во входном наборе данных.

• Пример: операции присваивания, сложения, взятия элемента списка по индексу и др.

2. Линейное время: \(O(N)\).

• Время выполнения пропорционально количеству элементов в коллекции.

• Пример: найти имя в телефонной книге простым перелистыванием, почистить ковер пылесосом и т.д.

3. Логарифмическое время: \(O(\log{N})\).

• Время выполнения пропорционально логарифму от количества элементов в коллекции.

• Пример: найти имя в телефонной книге (используя двоичный поиск).

4. Линейно-логарифмическое время: \(O(N \log{N})\).

• Время выполнения больше чем, линейное, но меньше квадратичного.

• Пример: обработка \(N\) телефонных справочников двоичным поиском.

5. Квадратичное время: \(O(N^{2})\).

• Время выполнения пропорционально квадрату количества элементов в коллекции.

• Пример: вложенные циклы (сортировка, перебор делителей и т.д.).

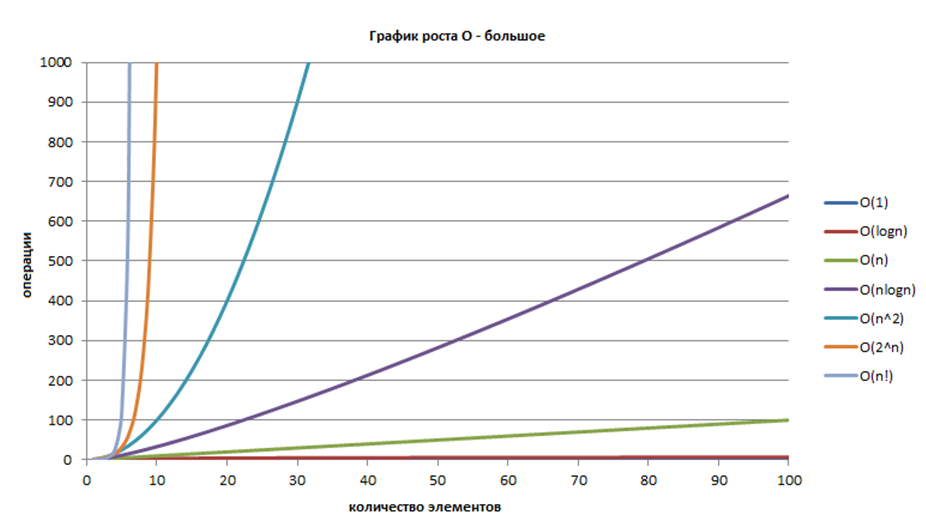
На Рисунке 6.1.1 приведен график роста \(O\)-большое.

Рисунок 6.1.1 - График роста \(O\)-большое 6

6.1.3. Оценка сложности алгоритмов

Для оценки вычислительной сложности алгоритмов необходимо знать и учитывать сложности:

• используемых структур данных;

• совокупности различных операций.

6.1.3.1. Операции над структурами данных

В Python имеются коллекции (структуры данных), операции над которыми имеют определенную сложность.

6.1.3.1.1. Список и кортеж

Большинство операций со списком/кортежем имеют сложность \(O(N)\) (Таблица 6.1.1).

Таблица 6.1.1 - Асимптотические сложности для списка или кортежа

Операция	Сложность	Примечание
len(lst)	\(O(1)\)
lst.append(5)	\(O(1)\)
lst.pop()	\(O(1)\)	Аналогично lst.pop(-1)
lst.clear()	\(O(1)\)	Аналогично lst = []
lst[a:b]	\(O(b-a)\)
lst.extend(...)	\(O(len(...))\)	Зависит от длины аргумента
list(...)	\(O(len(...))\)	Зависит от длины аргумента
lst1 == lst2	\(O(N)\)
lst[a:b] = ...	\(O(N)\)
del lst[i]	\(O(N)\)
lst.remove(...)	\(O(N)\)
x in/not in lst	\(O(N)\)	Поиск в списке
lst.copy()	\(O(N)\)	Аналогично lst[:]
lst.pop(i)	\(O(N)\)	Точнее \(O(N)\)
min(lst)/max(lst)	\(O(N)\)
lst.reverse()	\(O(N)\)
for v in lst:	\(O(N)\)
lst.sort()	\(O(N \log{N})\)	Направление сортировки не играет роли
k * lst	\(O(k \cdot N)\)

6.1.3.1.2. Множество

По сравнению со списком/кортежем множества большую часть операций выполняют со сложностью \(O(1)\) (Таблица 6.1.2).

Таблица 6.1.2 - Асимптотические сложности для множества

Операция	Сложность	Примечание
len(s)	\(O(1)\)
s.add(5)	\(O(1)\)
x in/not in s	\(O(1)\)	В отличие от списка, где \(O(N)\)
s.remove(5)	\(O(1)\)	В отличие от списка, где \(O(N)\)
s.discard(5)	\(O(1)\)
s.pop(i)	\(O(1)\)	В отличие от списка, где \(O(N)\)
s.clear()	\(O(1)\)	Аналогично s = set()
set(...)	\(O(len(...))\)	Зависит от длины аргумента
s != t	\(O((len(s))\)	Аналогично len(t)
s <= t	\(O(len(s))\)
s >= t	\(O(len(t))\)
s | t	\(O(len(s)+len(t))\)
s & t	\(O(len(s)+len(t))\)
s - t	\(O(len(s)+len(t))\)
s ^ t	\(O(len(s)+len(t))\)
for v in s:	\(O(N)\)
s.copy()	\(O(N)\)

6.1.3.1.3. Словарь

Большинство операций словарей имеет сложность \(O(1)\) (Таблица 6.1.3).

Таблица 6.1.3 - Асимптотические сложности для словаря

Операция	Сложность	Примечание
d[k]	\(O(1)\)
d[k] = v	\(O(1)\)
len(d)	\(O(1)\)
del d[k]	\(O(1)\)
d.method	\(O(1)\)
d.pop(k)	\(O(1)\)
d.popitem()	\(O(1)\)
d.clear()	\(O(1)\)	Аналогично s = {} или dict()
d.keys()	\(O(1)\)
dict(...)	\(O(len(...))\)	Зависит от длины аргумента
for k in d:	\(O(N)\)	Для всех методов: keys(), values(), items()

Примечание

Важно выбирать структуру данных, которая была бы оптимальной для конкретной задачи.

Например, если приложения будет осуществлять частый поиск информации, словарь даст большую эффективность, при этом, если необходимо просто хранить упорядоченный набор данных - словарь или кортеж подойдут лучше.

6.1.3.2. Закон сложения и умножения для \(O\)-нотации

Для оценки сложности совокупности операций используются законы сложения и умножения.

1. Закон сложения: итоговая сложность двух последовательных действий равна сумме их сложностей:

\[O(f(n)) + O(g(n)) = O(f(n) + g(n))\]

Особенности:

• итоговая сложность алгоритма оценивается наихудшим из слагаемых:

\[O(N) + O(\log{n}) = O(N + \log{n}) = O(N)\]

• в итоговой сложности константы отбрасываются

\[O(N) + O(N) + O(N) = 3 \cdot O(N) = O(N)\]

• при ветвлении берется наихудший вариант

  if test:     # O(t)
      block 1  # O(b1)
  else:
      block 2  # O(b2)
  

  \[O(N) = O(t) + max(O(b1), O(b2))\]

2. Закон умножения: итоговая сложность двух вложенных действий равна произведению их сложностей:

\[O(f(n)) + O(g(n)) = O(f(n) \cdot g(n))\]

# Общая                   O(N^2)
for i in range(N):      # O(N)
    for j in range(N):  # O(N)

6.1.4. Сравнение производительности работы алгоритмов

Как правило существует не один алгоритм, позволяющий решить требуемую задачу, поэтому при разработке алгоритма необходимо учитывать его вычислительную сложность.

В Листинге 6.1.1 приведен пример решений одной и той же задачи, используя алгоритмы с разной алгоритмической сложностью.

Листинг 6.1.1 - Примеры определения сложности алгоритмов | скачать

# 3 алгоритма, выполняющих одну и ту же задачу - проверку, что
# все значения списка различны - но имеющие разную вычислительную сложность

import random
import time


def timeit(func, *args, **kw):
    """Выполнить функицю 'func' с параметрами '*args', '**kw' и
    вернуть время выполнения в мс."""

    time_start = time.time()
    res = func(*args, **kw)
    time_end = time.time()

    return (time_end - time_start) * 1000.0, res


def is_unique_1(data):
    """Вернуть 'True', если все значения 'data' различны.

    Алгоритм 1:
      Пробежимся по списку с первого до последнего элемента и для каждого из
      них проверим, что такого элемента нет в оставшихся справа элементах.

    Сложность: O(N^2).
    """
    for i in range(len(data)):       # O(N)
        if data[i] in data[i+1:]:    # O(N) - срез + in: O(N) + O(N) = O(N)
            return False             # O(1) - в худшем случае не выполнится
    return True                      # O(1)


def is_unique_2(data):
    """Вернуть 'True', если все значения 'data' различны.

    Алгоритм 2:
      Отсортируем список. Затем, если в нем есть повторяющиеся элементы, они
      будут расположены рядом — т.о. необходимо лишь попарно их сравнить.

    Сложность: O(N Log N).
    """
    copy = list(data)                # O(N)
    copy.sort()                      # O(N Log N) - «быстрая» сортировка
    for i in range(len(data) - 1):   # O(N) - N-1, округлим до O(N)
        if copy[i] == copy[i+1]:     # O(1) - [i] и ==, оба по O(1)
            return False             # O(1) - в худшем случае не выполнится
    return True                      # O(1)


def is_unique_3(data):
    """Вернуть 'True', если все значения 'data' различны.

    Алгоритм 3:
      Создадим множество из списка, при создании автоматически удалятся
      дубликаты если они есть. Если длина множества == длине списка, то
      дубликатов нет.

    Сложность: O(N).
    """
    aset = set(data)                # O(N)
    return len(aset) == len(data)   # O(1) - 2 * len (O(1)) + == O(1)

# Проверка

res = [["i", "1 (мс.)", "2 (мс.)", "3 (мс.)"]]
for i in (100, 1000, 10000, 20000, 30000):
    # Из 100000 чисел выбираем 'i' случайных
    data = random.sample(range(-100000, 100000), i)

    res.append([i,
                timeit(is_unique_1, data)[0],
                timeit(is_unique_2, data)[0],
                timeit(is_unique_3, data)[0]])

print("{:>10} {:>10} {:>10} {:>10}".format(*res[0]))
for r in res[1:]:
    print("{:>10} {:>10.2f} {:>10.2f} {:>10.2f}".format(*r))

# -------------
# Пример вывода:
#
#         i    1 (мс.)    2 (мс.)    3 (мс.)
#       100       0.00       0.00       0.00
#      1000      15.01       0.00       0.00
#     10000    1581.05       5.00       2.00
#     20000    7322.86      12.01       2.00
#     30000   35176.36      25.02       8.01

Примечание

При написании алгоритмов стремитесь выбирать решение, обладающее наименьшей вычислительной сложностью.

---

1

Sebesta, W.S Concepts of Programming languages. 10E; ISBN 978-0133943023.

2

Python - официальный сайт. URL: https://www.python.org/.

3

Python - FAQ. URL: https://docs.python.org/3/faq/programming.html.

4

Саммерфилд М. Программирование на Python 3. Подробное руководство. — М.: Символ-Плюс, 2009. — 608 с.: ISBN: 978-5-93286-161-5.

5

Лучано Рамальо. Python. К вершинам мастерства. — М.: ДМК Пресс , 2016. — 768 с.: ISBN: 978-5-97060-384-0, 978-1-491-94600-8.

6

Знай сложности алгоритмов. URL: https://habrahabr.ru/post/188010/.